电感,电容,电阻
- T型去耦
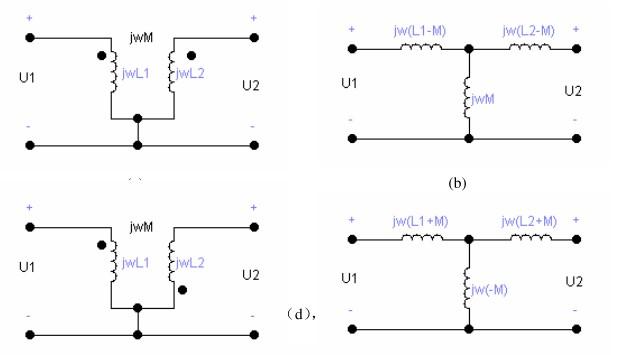
- 电阻、电感串算术、并调和、变压/流乘;电导、电容串调和、并算数、变压/流除
- 磁链守恒:对于一个纯电感回路,由 KVL $\Sigma L_k\frac{\text{d}i_k}{\text{d}t}=0$ 有 $\Sigma L_ki_k$ 守恒
- 电荷守恒:连到同一节点的电容, $\Sigma Q_k=\Sigma U_kC_k = Const$
- 时间常数 $\tau_C=RC, \tau_L=L/R$
- RLC:
串联 $R$ 并联 $G$ 过阻尼 $>2\sqrt{L/C}$ $>2\sqrt{C/L}$ 临界阻尼 $=2\sqrt{L/C}$ $=2\sqrt{C/L}$ 欠阻尼 $<2\sqrt{L/C}$ $<2\sqrt{C/L}$ 无阻尼 $0$ $0$ - 冲激响应 $h(T)=\frac{\text{d}S(t)}{\text{d}t}$
- 受控电源等效:与i有关项,需串联到对应路,然后等效电阻;u 项需并联到对应路, 然后等效电导;常数项直接等效为电源。注意方向:电流方向应为电压降向。
- 电容:从正流向负为正参考方向
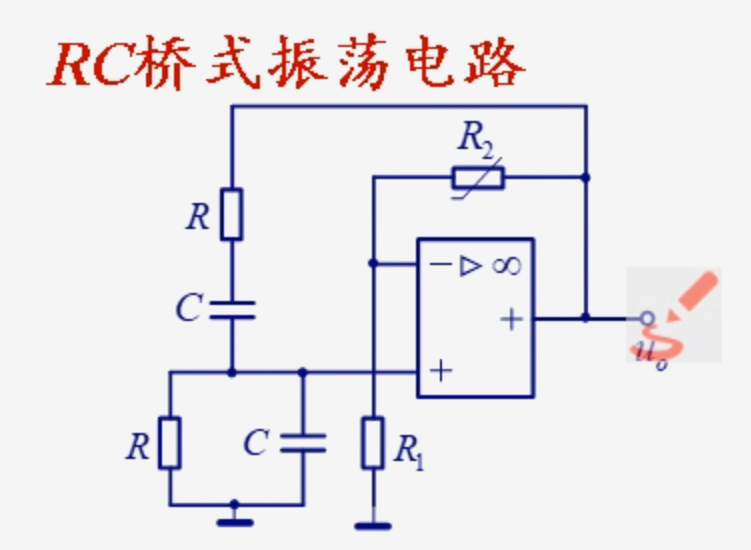
- RC 桥式振荡
拉普拉斯变换
$F(s)=\int_{0^-}^\infty f(t)e^{-st}\text{d}t$
$f(s)=\frac1{2\pi j}\int_{\sigma-j\infty}^{\sigma+j\infty} F(t)e^{st}\text{d}t, t\ge0$
常见变换表:
| 原函数 | 像函数 |
|---|---|
| $\delta(t)$ | $1$ |
| $\varepsilon(t), 1$ | $1/s$ |
| $t^n$ | $n!/s^{n+1}$ |
| $\cos(\omega t)$ | $\frac{s}{s^2+\omega^2}$ |
| $\sin(\omega t)$ | $\frac{\omega}{s^2+\omega^2}$ |
| $e^{-at}$ | $1/(s+a)$ |
性质:
- 线性性显然
- 微分: $\frac{\text{d}f(t)}{\text{d}t}$ -> $sF(s)-f(0^-)$
- 积分: $\int_{0^-}^tf(\tau)\text{d}\tau$ -> $F(s)/s$
- 时移: $f(t-\tau)$ -> $e^{-s\tau}F(s)$
- 频移: $e^{\alpha t}f(t)$ -> $F(s-\alpha)$
常见元件
| 元件 | 阻抗 | 等效电压源 |
|---|---|---|
| $R$ | $R$ | $0$ |
| $C$ | $1/sC$ | $u/s$ |
| $L$ | $sL$ | $Li$ |
对于互感,等效为 $sMi_2$ 的受控电压源,方向为阻碍电流方向。电流从点端流入。 对于电源,值变为 $1/s$ 倍
卷积定理:零状态响应 $y(t)=\int_{-\infty}^\infty exc(\tau)h(t-\tau)\text{d}\tau$ 其中 $h(t)$ 为该电路的冲激响应。 由拉普拉斯变换,有 $Y(s)=F(s)H(s)$
终值/初值定理:
- $\lim_{t\to\infty}f(t)=\lim_{t\to0}sF(s)$
- $\lim_{t\to0}f(t)=\lim_{t\to\infty}sF(s)$
