misc

  • 密码：
    • （密码法）采用特定变换的方法对信息等进行加密保护、安全认证的技术、产品和服务
    • 是研究密码技术（Cryptography）和密码分析（Cryptanalysis）的技术科学
    • 密码体制是满足条件的五元组 $\mathcal{P,C,K,E,D}$
  • Kerckhoffs原则：密码体制的安全性仅依赖于密钥，其他一切（包括算法本身）都是公开的。
  • 香农的保密系统理论
    • 无条件安全：m 明文，c 密文，有 $I(m;c)=0, H(m|c,k)=0, H(c|k=k_0)=H(m)$ （第三条仅对于一一映射代换成立）
    • 计算安全：各种攻击方法的复杂度均超出了分析者的计算资源可达到的合理边界
  • 攻击模型：唯密文攻击，选择明文，已知明文，选择密文
  • 法律法规：电子签名法 (2004)，网络安全法 (2016)，密码法 (2019)，数据安全法 (2021)，个人信息保护法 (2021)

古典密码

  • 古典代换
    • Caesar cipher: +3
    • Vigenere: 多单字母P
    • 密码机
    • 中国古代 反切码：诗为密钥，声母-韵母-声调
  • 古典置换
    • Scytale：棍子
    • 平面轨迹
      • 轨道栅栏 Rail Fence
      • 几何图形
    • 行变换：
      • 以密钥（循环）给出的顺序按行读出密文
      • 英文密钥：按字母大小顺序
      • 密码分析：猜测密钥周期, 再对可能的行列变换进行猜测
    • 中国古代：藏头诗

序列密码

  • 冷战时期受政治影响大，大部分研究保密
  • 原理：密钥流 xor 明文
  • 结构：
    • 同步流密码：独立于明文，但不可抗缺码
    • 自同步：密钥唯一，$g_n$ 仅依赖于上 n 个 c； $c_{i-k..i-1} \to g_n \to m_i \to c_i$
  • LFSR:
    • $f=\sum^\oplus c_ia_i$ 作为下一个 $a_{n}$，联接多项式为 $1 + \sum_1^n c_{n+1-i}x^i$
    • 左 an c1 右 a1 cn；左进右出
    • 最长：
      • m序列：$n$ 级 LFSR 产生周期为 $2^n-1$ 的序列
      • 条件：联接多项式不可约（必要）；$F_2$ 上本原多项式（充要）；$2^n-1$ 素且不可约（充分）
      • 随机性：
        • $0,1$ 分别出现 $2^{n-1}-1, 2^{n-1}$ 次
        • 长 $k$ 游程有 $2^{n-2-k}\ (1\le k\le n-2)$ , 长 $n-1$: 0, 长 $n$: 1
        • $C(\tau)=-1$
    • 对 $n$ 级，$2n$ 明密文对可破解，计算量 $n^3$ （矩阵逆）
  • Golomb 随机假设：
    • 周期内 0,1 个数相等
    • 长 i 游程（bit 连续相同）占 $2^{-i}$
    • （注意到 $\sum_1^{\infty}k\cdot 2^{-k}=2$ 游程总数应接近周期一半，考虑 0,1 概率相等，应有长 $k$ 的0/1游程个数为 $\frac{T}{2}\cdot 2^{-i}/2 = T\cdot 2^{-i-2}$）
    • $C(\tau)=\sum_i^n (-1)^{a_i+a_{i+\tau}}=常数$ $(\tau \ne 0 \mod n)$ （对于不同 $\tau$ 有 $(a_i,a_{i+\tau})$ 分布相同）
  • 线性复杂度：能够生成该序列的最短 LFSR 的长度；决定了破译复杂度
  • 好密码：周期长，随机性好，线性复杂度大（周期一半）
  • 生成器：
    • 滤波：由 LFSR 单输出非线性滤波
    • 组合：多个 LFSR 加非线性组合
    • 钟控/停走：LFSR 控钟+LFSR 被控
  • 其他生成器：
    • 勒让德序列：$p$ 为奇素数，$a_i=(\exists x\in \mathbb{N}\quad s.t.\quad x^2\equiv i \mod p)$
    • 椭圆曲线（TODO）
  • 实用流密码：
    • 钟控+停走 (A5)
    • RC4：
      • 初始化：(sbox, key) -> sbox 赋值 0-255 + 利用 key 随机打乱 (j+=s[i]+k[i])
      • 加密：每 byte 同步打乱 sbox 生成密钥流 j += s[i]

分组密码

  • 设计原理：充分利用简单轮函数和非线性变换进行若干轮迭代
    • 乘积组合：多种简单运算组合，包括置换、替换，e.g. 异或、线性变换、模乘
    • 混淆：密文统计特征与密钥关系复杂化
    • 扩散：明文/密钥任何一位都影响密文多位；雪崩/完备特性
  • Feistel 结构：(↙方向传递)
    • $L_i, R_i = R_{i-1}, L_{i-1}\oplus f(R_{i-1}, k_i)$
    • $L_{i-1}, R_{i-1} = R_{i}\oplus f(L_i, k_i), L_i$
  • DES 64b block, 56b key
    • 初始置换/逆置换 $P_I$；64->64；output[i]=input[PI[i]]
    • 轮函数 （16）：
      • 扩展 E；32->48；output[i]=input[E[i]]
      • 异或 k_i；48->48
      • S盒；6x8->4x8；output_k[i]=S_k[input_k[1,6],input_k[2-5]]
      • P 盒；32->32；output[i]=input[P[i]]
    • 子密钥
      • 长为 64 但每 7bit 有奇偶校验位 （和为奇）
      • 置换 PC-1；64->56；output[i]=input[PC1[i]]
      • 每轮前 LS；28x2->28x2；output_k[i] = rol(input_k[i], LS[k])
      • 每轮密钥通过置换 PC-2 产生；56->48；output[i] = input[PC2[i]]
    • 弱性质
      • 互补：$\bar c = \text{DES}_{\bar k}(\bar m)$
      • 弱密钥 DES(DES(m))=m：01, 1F 以及补
  • IDEA 64b block, 128b key
    • 基本运算：异或 $\oplus$，模 $2^{16}$ 加 $\boxplus$，模 $2^{16}+1$ 乘 $\odot$
    • MA 单元 (32, 16, 16)->32 
      def ma(a1, a2, k1, k2): # all uint16, override with mod plus / mul
	s = a1 * k1
	t = (s + a2) * k2
	return s + t, t
    • 轮函数 （8.5）
      • 初始运算 output[i]=[mmul,mplus,mplus,mmul][i](input[i], k[i])
      • MA t1, t2 = ma(input[1]^input[3],input[2]^input[4], k5, k6)
      • output[1,3] ^= t2, output[2,4] ^= t1
      • swap(output[2],output[3])
    • 输出变换即轮函数的初始变换
    • 密钥生成：一次生成 8 个 (16x8)，不够 rol25 再生成；不与轮同步 8x6+4
    • 解密密钥：解密循环 I 的头4个子密钥从加密循环 10－I 的头4个子密钥中导出；解密密钥第1、4个子密钥对应于1、4加密子密钥的乘法逆元；2、3对应2、3的加法逆元 （TODO）
    • 注：和 Feistel 一样构造了使用非可逆变换（ma），但有可轮间传递数据的结构（使用异或 ma 结果使 output[1]xor output[3]=input[1] xor input[3] 抵消了 ma）；密钥生成有些简陋了。
  • AES / Rijindael: 128bit block, 128-256bit key (10,12,14 cycles)
    • State: 8bit 为字，4 行，4 列, 128bit
    • 子密钥生成：
      • 轮密钥不与轮同步，由密钥扩展随取随用
      • 10/12/14 轮
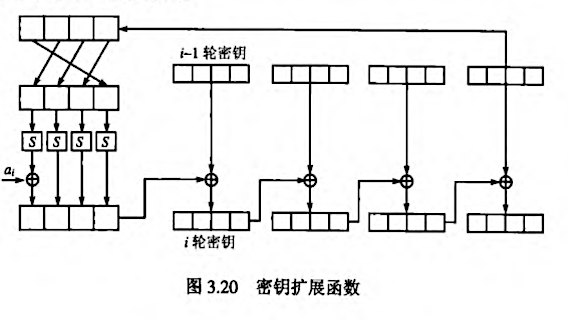
      • aes prf
    • 轮函数 列长为 r
      • 字节替换/S 盒； 4rx8 -> 4rx8
      • 行移位；4xrx8 -> 4xrx8；rol i (by byte)
      • 列混合；每列视为多项式 $\sum_0^{r-1} a_i x^{r-i-1}$，做 $x^4+1$ 模乘
        • 可视为系数 ror 的矩阵乘（$GF(2^8)$ 上，模 0x1B；可查表 (02, 03, 0e, 0b, 0d, 09 共 6*256 空间 / embed 算 *2 然后霍纳法则)，可逆；
      • 轮密钥加
  • 工作模式：
    • ECB：逐块
    • CBC：有 IV，$C_{i+1}=f(M_{i+1}\oplus C_i)$；错误传播本块+后一块对应 bit
    • CFB-n：有 IV，$C_i=M_i\oplus f(IV_{i-1}[:n]), IV_i=IV_{i-1}«n | C_i$；寄存器长度与算法一致；错误传播 L/n 块，错误的那块只改对应 bit
    • OFB-n：同 CFB 但把加密算法输出直接反馈；错误仅影响对应 bit
    • CTR：可并行，$C_i=M_i\oplus f(IV+i)$
    • GCM：CTR + GHASH；先 CTR 完，用 K 派生的 H，预定文本 A，密文 C 计算 GHASH $X_{m+n+1}$ where $X_{i}=(X_{i-1}+ S_i)\cdot H$ （$GF(2^{128})$ 内运算，mod 0x87），$S$ 为 $(A||pad||C||pad||len(A)||len(C))$
  • 算法分析
    • 强力攻击（分类：唯密文，已知明文，选择明/密文，自适应选择明/密文）
    • 差分攻击：依赖 S 盒的差分熵低（概率分布不平均），寻找概率最高/0路径

公钥密码

  • 对称缺陷：密钥管理分配麻烦，认证（抗抵赖）
  • 分类：
    • 公钥分发 Public-Key Distribution Schemes
    • 公钥加密 Public Key Encryption
    • 数字签名 Signature Schemes
  • 特点：
    • 加密公开，解密保密
    • 公钥+密文 -x> 明文 （=> 公钥 -x>私钥）
    • 攻击：强力，选择消息，私钥破解
  • 陷门单向函数
    • $f$ 容易 $f^{-1}$ 难
    • （最重要！）$F_p$ 上离散对数问题 $y=x^b$
    • （非循环交换群）离散对数问题 $y=x^b$ （认为等价于大素数乘积分解）
    • （非循环交换群）二次剩余问题 $y=x^2$
  • Diffie-Hellman 密钥交换
    • 单向性：$F_p^*$ 上离散对数
    • 生成元 $g$，生成随机 $x_A, x_B$, 交换 $y_A=g^{x_A}, y_B=g^{x_B}$，则共享密钥为 $y_A^{x_B}=y_B^{x_A}$
  • El Gamal 公钥密码
    • 单向性：$F_p^*$ 上离散对数
    • 密钥生成：大素数 $p$，$g$ 是 $F_p^*$ 生成元，任意 $x<p-1$ 为私钥，$g, y=g^x\mod p$ 为公钥
    • 明文空间 $F_p^*$，密文空间 $F_p^*\times F_p^*$
    • 加密：任取 $k$（保密），$c=(g^k, my^k) \mod (p,p)$
    • 解密：$m=c_2c_1^{-x}$
      • 算法：由费马小定理，$c^{-x}=c^{-x \mod p-1}$ / 扩展欧几里得算法
    • 签名：
      • 选 $k\text{ s.t. } GCD(k,p-1)=1$
      • $K=a^k, S=k^{-1}(h-xK)\pmod{p-1}$，$(K,S)$ 为 $h$ 签名
      • 验签：$y^{K}K^{S}\equiv a^h \pmod{p}$
      • 注：$k$ 的选择并非任意，这很重要！因此才有了 DSA 改进
  • DSA 签名算法
    • 密钥生成：N bit $p$, L bit $q$ 使得 $q|p-1$；$g=h^{\frac{p-1}{q}}\pmod{p}$；选择私钥 $x<q$ 计算公钥 $y=g^x\pmod{p}$
      • 注：ECDSA 没有这么多要求，随便选 g,p,q；主要是 $\mathbb{Z}^*_p$ 的阶是 $p-1$ 为和数，就很难受
    • 签名：
      • 选 $k<q$
      • 签名：$K=(g^k\text{ mod }p) \pmod{q}$，$S=k^{-1}(h+xK)\pmod{q}$
      • 验签：$K$ 等于 $((y^{K}g^{h})^{S^{-1}}\text{ mod }p) \pmod{q}$ （注：指数上可以 $\text{mod }q$ 优化）
      • 注：这里的 K 由于 mod q 了，从 $\langle g\rangle$ 群降维到了 $F_q$，之后不涉及 $\langle g\rangle$ 相关性质。
  • Rivest-Shamir-Adleman 公钥密码
    • 单向性：风味离散对数
    • 密钥生成：生成大质数x2: $pq=n$，生成随机数 $e\le\phi(n)$ 计算 $d=e^{-1} \mod \phi(n)$；则 $(e,n), (d,p,q)$ 为公钥、私钥
    • 加解密：$c=m^e, m=c^d \mod n$
    • 签名：$S=h^d, S’=S^e$
    • 工程上：
      • 私钥文件会存储所有参数
      • $e=65535$
    • 中国剩余定理优化解密
      • 原解密计算复杂度：$\log{d}$ 次乘法，每次乘法 $\log^2 n$ FLOP （忽略加法）；共 $\log d\log^2n$ FLOP
      • 由费马小定理 $c^{p-1}=1 (\text{mod}\ p)$，$c^d=c^{d\mod (p-1)} \mod p=m_p$；由此可在 $\log p \times \log^2 p$ FLOP 计算 $m_p$；$m_q$ 同理；共 $2\log^3p$ FLOP
      • 此时 $m=m_p\mod p = m_q \mod q$；由中国剩余定理，令 $t_p=(q^{-1}\mod p)$, $t_q=(p^{-1}\mod q)$（都可以提前计算），有 $m=m_pq^{-1}_p q + m_q p^{-1}_q p \mod n$；计算量可忽略
      • 可见考虑 $d\sim n\sim p^2$ 的情况下，能快 4 倍左右；代价是要知道完整的 $p,q,p^{-1}_q, q^{-1}_p$
    • 攻击：共模攻击，弱指数攻击
    • EC 可用性：$pq$ 阶 $\langle G\rangle$ 不够安全且难以找到符合条件参数
  • SM2
    • 单向性：离散对数
    • 密钥生成：大素数 $p$，$g$ 是生成元，任意 $k<p-1$ 为私钥，$q=kg$ 为公钥 （同 ElGamal）
    • 加解密：
      • DH：加密者任意生成 $r$，则 $rq$ 为共享密钥 $S$，且只需传输 $rg$
      • KDF：通过 $S$、消息长度派生出密钥
      • Hash：SM3 $(S_x||M||S_y)$ 得哈希，拼接在最后
      • 加密：M 通过 xor 派生密钥加密
      • 解密：xor 得 M 后 验签
      • 密文数据：$(rg || C || Hash)$
    • 注：SM2 启示我们，只要有好的密钥交换算法、密钥派生和对称加密就可以实现公钥加密： 可以把预生成 a,A 中 A 公开，这样对方只要随机生成 b B, 用 KDF(A,b) 加密，把 B 绑到密文中，A 可以用 KDF(a,B) 解密。但签名就不行了，因为是单向的。
  • Rabin
    • 单向性：二次剩余问题
    • 密钥生成：$p\equiv q \equiv 3\mod 4$，$n=pq$ 为公钥，$p,q$ 为私钥
    • 加解密：$c = m^2 \mod n, m= \pm(c^{\frac{p+1}{4}} \mod p)q q^{-1}_{p} \pm (c^{\frac{q+1}{4}} \mod q) p p^{-1}_{q} \mod n$；
      • 注：有四种可能明文，需要可识别
      • 又是中国剩余定理
      • 是 $e=2$, 不满足 $\exists d, de\equiv 1 \mod \phi(n)$ 的 RSA。
    • 选择密文攻击不安全
  • Elliptic Curve (over Finite Fields) (ref)
    • 是一系列 $F_p\times F_p$ 子集上的质阶交换群（因此适用离散对数问题对应算法）
    • 通常选用曲线 $y^2=x^3+ax+b, 4a^3+27b^2\ne 0\mod p$；参数包括 $p, a, b, G$；以及导出参数 $n=|\langle G\rangle|, h=\frac{\# E(F_p)}{n}$
    • 质数阶循环群二次剩余问题有 $O(\log^2 p)$ 快速算法，可以由 $x$ 推算出 $y$。
    • 任意选择参数和基点 $G$，使满足：$\#E(F_p)$ 是一个素数或近乎素数，$|G|$ 是大素数（最好等于 $\# E(F_p)$，最好 $h=1$；由此构成的 $\langle G\rangle$ 作为群集合；当 $h=1$ 时有 $\# E(F_p)=\langle G\rangle \cong Z_{n}$。
    • 法则 （全部 $\text{mod}\ p$）
      • 单位元/无穷远点 $\mathcal{O}$
      • 逆元 $-P = (x_1, -y_1)$
      • 加法 $\lambda = \begin{cases}\frac{y_2 - y_1}{x_2 - x_1} & \text{if } P \neq Q \ \frac{3x_1^2 + a}{2y_1} & \text{if } P = Q\end{cases}$，$\begin{pmatrix} x_3 \\ y_3 \end{pmatrix} = \begin{pmatrix} \lambda^2 - x_1 - x_2 \\ \lambda(x_1 - x_3) - y_1 \end{pmatrix}$
    • Elliptic Curve Cryptography：
      • EC+El Gamal：课上讲了，但工程上没人用
      • 签名 ECDSA；密钥交换 ECDH(E)…
      • ECMQV （TODO）
  • 其他：
    • $GF(2^n)$ 上的，NTRU…
    • McEliece 公钥密码：线性译码问题（TODO）
    • 背包问题 （TODO）
  • 攻击：
    • 共模攻击
    • …

认证和哈希

  • 目的：身份确认，防篡改重放延迟（完整性）
  • 安全要求
    • 单向性/抗原像：无法计算 $y$，$H(y)=h$
    • 弱抗碰撞性/第二抗原像：无法计算找到 $y$， $H(y) =H(x)$
    • 强抗碰撞：无法计算找到任何 $x,y$，$H(x)=H(y)$
  • 认证方法：加密/MAC/哈希
    • MAC 需要 sk 可以认证消息合法；hash 搭配非对称加密可以提供不可否认性（签名）
    • MAC：基于哈希，基于分组密码，加密认证模式
      • HMAC：$Hash((K\oplus opad) || Hash(K\oplus ipad)||M)$
      • DES Based: CBC 模式最后输出
  • 两种结构
    • Merkle–Damgård construction: $CV_{i}=f(M_i, CV_{i-1})$
    • 海绵结构：位宽(b)大于比特率(r)，$CV_i=f(CV_{i-1}\oplus M_i)$ 吸收，挤压 $CV_i=f(CV_{i-1})$ 每次 r bit 直到预定长度；安全性等于容量 c/2 (c+r=b)
  • MD5：
    • 512bit 分组，128bit state；4 轮 x 16 步
    • 结构：
      • pad and length: 填充一个 1 和若干 0 到 -64 mod 512 再填 64bit LE 长度
      • $IV$ 用LE常数
      • $F$ 为 HMD5(M,CV)+CV
    • HMD5 (see rfc1321)
      • M(k,i)=M[[k, 1+5k,5+3k, 7k][i]&0xf] （考虑 M 为 32 bitx16，注意这里 i, k 从 0开始，不同于书）
      • T(k,i)=2^32 abs(sin(16i+k+1)) （打表64）
      • g_i=[xy|!xz, xz|y!z, x^y^z, y^(x|!z)][i]
      • for i in 0..4, for k in 0..16:
        • $A = (A + g_i(B,C,D)+M(k,i)+T(k,i)) « s(k,i) + B$
        • A,B,C,D = D,A,B,C
  • SHA1：
    • 512bit 分组，160bit state；4 轮 x 20 步
    • 结构：同 MD5
    • HSHA：
      • M(k,i)=M[[k, 1+5k,5+3k, 7k][i]&0xf] （考虑 M 为 32 bitx16，注意这里 i, k 从 0开始，不同于书）
      • M(j)= j<16 ? M[j] : rol(M(j-16)^M(j-14)^M(j-8)^M(j-3), 1)
      • g_i=[xy|!xz, x^y^z, xy|yz|xz, x^y^z][i]
      • for i in 0..4, for k in 0..20:
        • E = E + g_i(B,C,D)+rol(A,5)+M(20*i+16)+T(i)
        • A,B,C,D,E = E, A, rol(B, 30), C, D
    • SHA2 / SM3：都是 MD5 改版（TODO） 
      algorithm  SHA-1  SHA2-256  SHA2-384  SHA2-512 SM3
digest     160    256       384       512      256
maxm(2^?)  64     64        128       128      64
block      512    512       1024      1024     512
word       32     32        64        64       32
steps      80     64        80        80       64
security   80     128       192       256      128
  • SHA3：
    • 结构：
      • 填充 10*1 （正则表达式）
      • f 是S盒
    • 实例 (b=1600) 
      name  S224  S256  S384  S512  SHAKE128  SHAKE256
d     224   256   384   512   /         /
r     1152  1052  832   576   1344      1088
c     448   512   768   1024  256       512
    • Keccak-f[1600]
      • 24轮迭代，每轮 5 步 ι ◦ χ ◦ π ◦ ρ ◦ θ

后量子密码

  • 量子算法
    • Shor 算法离散在多项式时间对数问题/大质因数分解问题：现有公钥算法不能用了
    • Grover 算法能把所有 $O(2^n)$ 遍历比较问题加速到 $O(2^{n/2})$：对称加密/哈希算法长度加倍
  • 后量子密码
    • 可以抵御已知量子计算攻击的公钥密码
  • 格 (lattice) 密码
    • 可以密钥交换、签名、加密
    • 运算空间：$n$ 维线性空间
    • 难题：SVP 最短向量问题，给定基，找出格中的最短非零向量；变体：
      • ASVP 近似最短向量问题
      • SIVP 最短线性无关向量问题
      • uSVP 唯一最短向量问题
      • CVP 最近向量问题
    • 实用算法：NTRU （TODO）
  • 基于编解码的密码（TODO）
    • GPT 公钥加密：基于线性最大秩距离码
    • McElice 公钥密码：基于 Goppa 纠错码
  • 基于二次多变量多项式
    • 公开 $L_2\circ F \circ L_1$ 用于加密，私钥是可逆的 $L_1,L_2$ 和$F$ （TODO）
  • 基于哈希和对称性：（TODO）
    • 可以签名
    • 通过哈系树构造；安全性基于抗碰撞性
    • Merkle 哈希树…
  • 基于安全多方计算：可以签名（TODO）

考点

  • 题型：
    • 填空题：非常简单，送分题！
    • 选择题：也非常简单！两分钟做完！
    • 问答题/简答题
  • 古典密码：代换置换
  • 对称密码
    • 现代分组：雪崩/混淆 (S)，完备/扩散 (P)
      • 乘积密码：SPN
      • Feistel 结构
      • 参数选择，安全效率兼顾——密钥长度，分组长度，迭代轮数，密钥编排，F 复杂度
      • IDEA, DES, 重点：AES 参数 (10-12-14)
      • 加密模式 EBC CBC OFB CFB CTR; 错误传播，仅加密/也要解密
    • 序列：
      • 安全性好的密钥流：周期，伪随机性（Golomb：01 等量，游程指数下降，自相关函数恒定），线性复杂度高
      • LFSR 原理，周期 ($2^n-1$)；提高线性复杂度（滤波，钟控/走停）
      • 知道有 RC4
  • 公钥
    • 数学困难问题：大整数分解，二次剩余，离散对数，椭圆曲线
    • 算法：RSA Rabin ElGamal ECDH；安全性（什么时候不安全）、正确性分析
      • RSA: 安全性基于计算 ø(N) 的困难性
        • 共模攻击：同消息、不同 e、同模计算的密文可 (Euclidean) 解出明文 （用 $re_1+se_2=1\pmod{n}$ 绕开 $d$）
        • 低加密指数广播攻击：同消息，同小 e，e 个不同互素 n，可由三密文+CRT+开 e 次方解明文
        • 低加密指数暴力攻击：算 $\sqrt[e]{c+kN}$ 直到为整
      • Rabin: 安全性基于（非素模）二次剩余问题 / n 因数分解；
        • 选择密文攻击 1/2 概率直接解私钥
      • El Gamal: 安全性基于离散对数
      • DSA: 共享 k 两条消息直接解私钥
    • ECDH 的主动攻击（mimt）
    • RSA 的中国剩余定理优化
  • 哈希函数
    • 认证的需求、目的：身份确认，防篡改重放延迟
    • 设计 不同场景 要怎么设计实现；场景设计
    • 安全要求：抗 原像，强弱碰撞
    • 两大类：MD（要掌握），海绵
    • 算法 分组长度、输出长度、迭代轮数